Мы можем найти аналитическое представление
Шаг 2
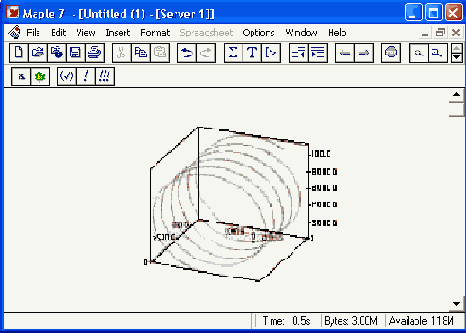
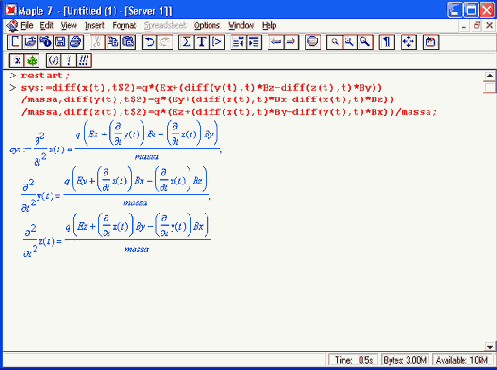
Мы можем найти аналитическое представление для траектории частицы в виде параметрически заданной (с параметром времени t) системы из трех уравнений:
Шаг 2
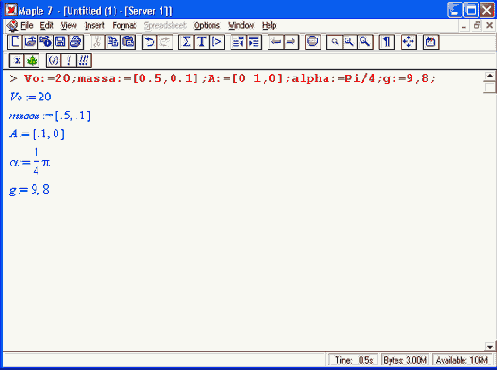
Шаг 2
> q:=1.6e-19:V:=le4:
> Vx:=V*cos(a1pha):Vy:=V*sin(a1pha):Ex:=0:Ey:=0:Ez:=0:Bx:=0: By:=0:Bz:=le-2:
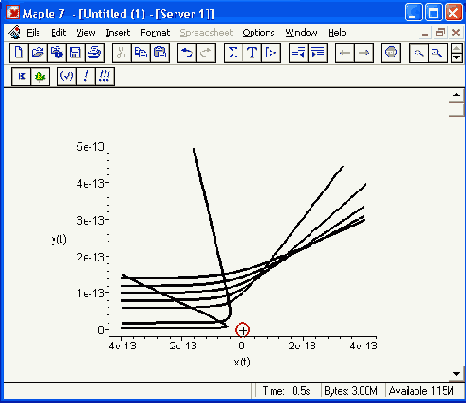
Выполним решение составленной выше системы дифференциальных уравнений:
Шаг 2
Шаг 2
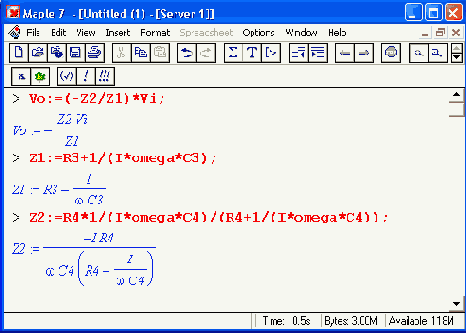
> omega := 2*Pi*f;
W := 2пf
Найдем коэффициент передачи фильтра и его фазо- частотную характеристику как функции от частоты:
> gain := abs(eva1c(Vo/Vi)):
> phase := evalc(op(2,convert(Vo/Vi.polar))):
Для просмотра громоздких аналитических выражений для этих параметров замените знаки двоеточия у выражений для gain и phase на знак точки с запятой. Далее введем конкретные исходные данные для расчета:
> R3 :=1000:
> R4 := 3000:
> СЗ :=0.08*10^(-6):
> С4 := 0.01*10^(-6):
Построим АЧХ фильтра как зависимость коэффициента передачи в децибелах (dB) от частоты f в Гц:
> plot(DogWf), 20*log10(gain), f=[10..50000], color=black, title='Коэффициент передачи dB как функция от частоты f в Гц'):
Эта характеристика представлена на Рисунок 17.17. Здесь полезно обратить внимание на то, что спад усиления на низких и высоких частотах происходит довольно медленно из-за малого порядка фильтра.
Шаг 2
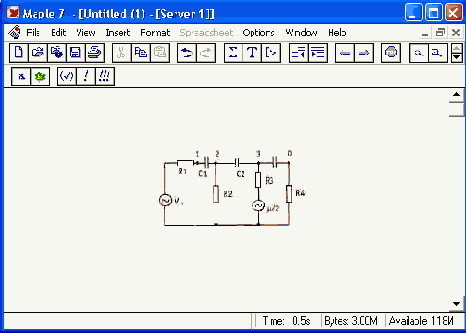
б
Рисунок 17.12. Принципиальная (о) и эквивалентная(6) схемы усилителя на полевом транзисторе
Наша цель заключается в расчете характеристик усилителя операторным методом. Подключим нужный нам пакет plots:
> restart:with(plots):
Warning, the name changecoords has been redefined
Из законов Киргофа вытекает, что сумма токов, втекающих в каждый узел и вытекающих из него равна 0. Следовательно, для узлов эквивалентной схемы Рисунок 17.12 можно записать следующую систему уравнений в операторной форме:
Шаг 2
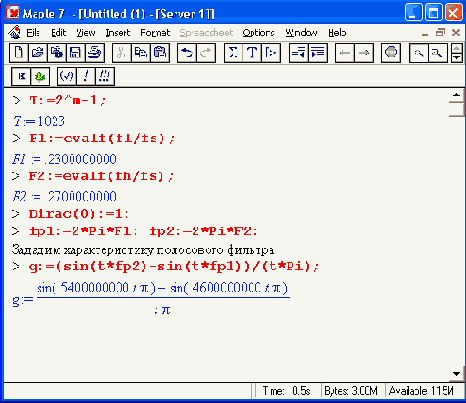
> С :-=(n) -> limit(g,t=n):h := aray(0..N): N2:=N/2:
> for n from 0 to N2 do h[N2-n]:= evalf(C(n)); h[N2+n] := h[N2-n]; od:
Определим массивы входного x(n) и выходного у(n) сигналов:
> х := array(-N..T): y := аггау(0..Т):
Установим значение х(n) равным 0 для времени меньше 0 и 1 для времени >=0:
> for n from -N to -1 do x[n] := 0; od:
> for n from 0 to Т do x[n] := Dirac(n); od:
Вычислим временную зависимость для выходного сигнала:
> for n from 0 to Т do y[n] := sum(h[k]*x[n-k],k=0..N): od:
Построим график импульсной характеристики фильтра, отражающей его реакцию на сигнал единичной площади с бесконечно малым временем действия:
> р := [seq([j/fs,y[j]],j=0..T)3:
> plot(p, time=0..3*N/fs, labels=[time,output], axes=boxed, xtickmarks=4, title-'Иипульсная характеристика фильтра',color=black);
Он показан на Рисунок 17.19. Нетрудно заметить, что эта характеристика свидетельствует об узкополосности фильтра, поскольку его частоты fl и fh различаются несильно. В этом случае полосовой фильтр по своим свойствам приближается к резонансному, хотя само по себе явление резонанса не используется.
Шаг 2
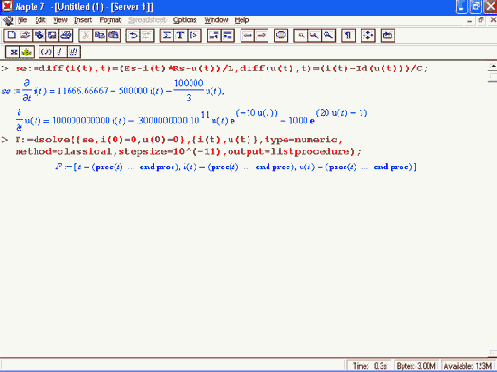
> gu:=odeplot(F,[t,u(t)],0,tm,color=black,
labels=['tVu(t),10*i(tr]):
> gi:=odeplot(F,[t,10*i(t)],0..tm.color-black):
> ge:=odeplot(F,[t,Es].0..tm.color=red): .
> display(gu.gi,ge);
Эти зависимости представлены на Рисунок 17.26. Из них хорошо видно, что цепь создает автоколебания релаксационного типа. Их форма сильно отличается от синусоидальной.
Шаг 2
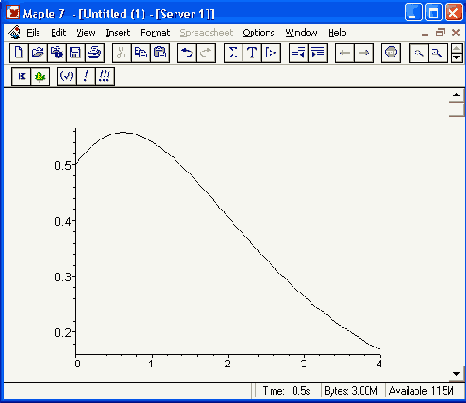
Итак, вычисление f(x) по ее интегральному представлению совершенно не эффективно. Наша цель состоит в разработке процедуры вычислений, которая дала бы 6 точных цифр результата в интервале [0..4] и требовала, по возможности, наименьшего числа арифметических операций для каждого вычисления. Втайне не вредно помечтать о том, чтобы после аппроксимации время вычислений уменьшилось бы хотя в несколько раз. Что получится на деле, вы увидите чуть позже. А пока войдем в дебри аппроксимации.
Шаг 2
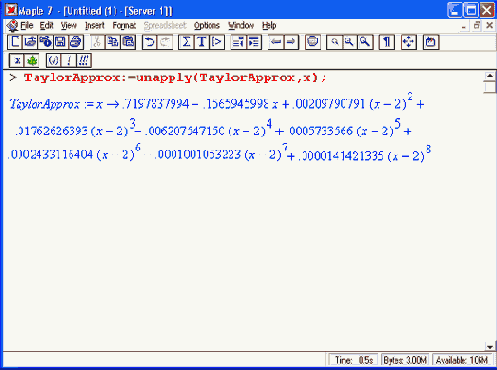
> plotd(f- TaylorApprox,0..4,.co1or=black);
и имеет вид, представленный на Рисунок 17.2. Эта кривая нас, прямо скажем, не слишком радует, поскольку погрешность в сотни раз превышает заданную.
Шаг 2
Шаг 2
Шаг 2
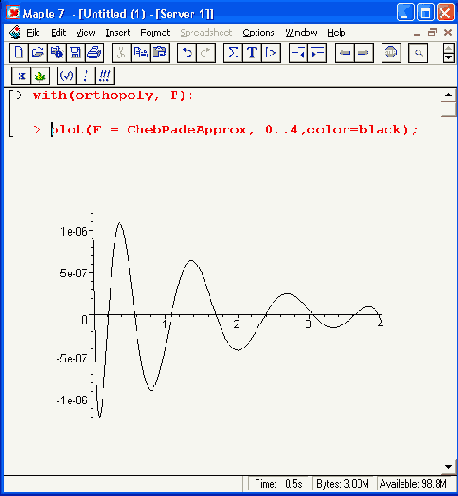
> maxChebPadeError :=abs( F(0) - ChebPadeApprox(O) );
maxChebPadeError= .1236746 10-5
Мы достигли впечатляющего успеха и остается сделать еще один шаг в направлении повышения точности аппроксимации.
Шаг 2
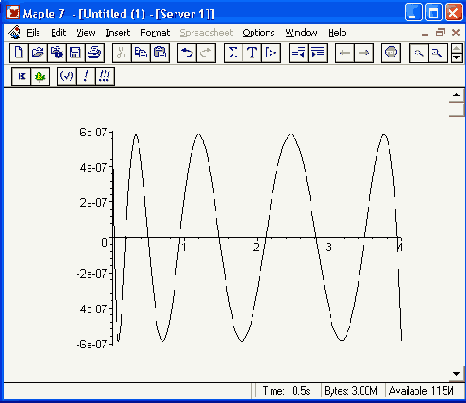
Таким образом, мы добились блестящего успеха в снижении погрешности до требуемого и довольно жесткого уровня. Если бы мы задались целью получить только четыре или пять точных знаков аппроксимации, что в целом ряде случаев вполне приемлемо, то могли бы получить нужный результат гораздо раньше. Нам остается оптимизировать полученную аппроксимацию по минимуму арифметических операций и проверить реальный выигрыш по времени вычислений.